Electric charges and fields

 

Electric Charges and Fields

 17-   Problems

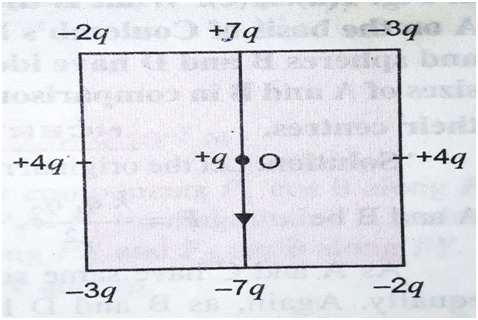
Question1. A particle carrying charges +q is held at the center of a square of each side one meter. It is surrounded by eight charges arranged on the square as shown in the figure. If q= 2 μC, what is the net force on the particle?


Solution. As is clear from figure, force on the particle at 0 due to (-2q, -2q); (-3q,-3q) and (+4q, +4q) are equal and opposite. They cancel out in pairs. However, the force due to +7q and -7q add up. Therefore, the net force on the particle at 0 is


Question2. Coulomb’s law for the electrostatic force between two point charge and Newton’s law for gravitational force between two stationary point masses, both have an inverse square dependence on the distance between the charges/masses.

(a) Compare the strength of these forces by these forces by determining the ratio of their magnitude (1) for an electron and a proton (2) for two protons

(b) Estimate the acceleration for electron and proton due to the electrical force of their mutual attraction when they are 1A0 apart.



Question3. Two electrons and a positive charge q are held along a straight line. At what position and for what value of q will the system be in equilibrium? Check whether it is stable, unstable, or neutral equilibrium.



Solution. Let two-electron of charge –e each be held at A and B. The third charge +q must be placed at the center O of AB. The forces on +q, due to two electrons being equal and opposite, cancel each other and it is in equilibrium.

For the charge(-e) at A to be in equilibrium, in the above figure, the force on the charge at A due to –e charge at B +force on charge at A due to +q charge at O=zero.



If charge at O is moved slightly toward A. It would not return to O on its own and shall continue to move toward A. Hence equilibrium is unstable.

Question4. Two equal positive charges, each of 2μC interact with a third positive charge of 3μC situated as shown in the figure. Calculate the magnitude and direction of the force on the 3μC charges.



Solution. In above figure

                                    OA = OB = 3m, OP = 4m

According to coulomb’s law,

Force on charge at P due to charge at A



F1 = 2.16 × 10-3 N, along with PA’, opposite to PA. It has two rectangular componetsF1 cos  along with PX and F1 sin  along with PY’. Similarly, the force on the charge at P due to charge at B, F2 = F1 (in magnitude). It is along PB’ opposite to PB. It also has two rectangular components: F2 cos  along with PX and F2 sin along with PY.                                  

 The components along with PY and PY’ cancel. The components along PX add up.

 The total force on 3 μC charges is

Question5. Find the magnitude of the resultant force on a charge of 1μC held at P due to two charge of +2×10-8C and -10-8C at A and B respectively.



In given figure                             AP = 10cm and BP = 5cm.

                                                    ∠APB = 900



Question6. Consider three charges q1, q2, q3 each equal to q at the vertices of an equilateral triangle of side l. What is the force on a charge Q (with the same sign as q) placed at the centroid of the triangle?


Solution. As shown in given figure, draw AD⊥BC.


Question7. Consider the charges q, q, and – q placed at the vertices of an equilateral triangle of each side l. what is the force on each charge?




Question8. Two fixed point charges +4e and +e units are separated by a distance a. Where should the third point charge be placed for it to in equilibrium?



Question9. Two pieces of copper, each weighing 0.01 kg are placed at a distance of 0.1m from each other. One electron from per 1000 atom of one piece of transfer to other pieces of copper. What will be the Coulomb force between two pieces after the transfer of electron? The atomic weight of copper is 63.5g/mole. Avogadro’s number = 6.25 × 1023 / gram mole.


For more information click.

https://www.blogger.com/blog/post/edit/2098949737310877088/508472146727475258



 


Comments

Post a Comment

please do not enter any spam link in the comment box

Popular posts from this blog

FORCE AND LAWS OF MOTION, Class IX, Part 4

Image
  If a boy wearing roller skates stands facing a wall and pushes the wall with his hands, the boy finds himself moving backward, away from the wall. It appears as if the wall also pushes the boy away. When the boy exerts a force on the wall by pushing it with his hands, then the wall exerts an equal force on the boy in the opposite direction . Since the boy is wearing roller skates, the opposite force exerted by the wall makes him backward, the boy on roller skates is exerting force on the wall towards the left side. The wall exerts an equal force on the boy towards the right side. Due to this, the boy moves in the backward direction. From this discussion, we conclude that when a boy exerts a force on the wall, the wall exerts an equal and opposite force on the boy . This is just an illustration of Newton’s third law of motion. Whenever one body exerts a force on another body, the second body exerts an equal and opposite force on the second body. The force exerted by the first bo
Read more

FORCE AND LAWS OF MOTION, Class IX, Part 3

Image
                                         In order to understand Newton’s second law of motion, we should first know the meaning of the term momentum of a moving body (or moving object). We know that a cricket ball is much heavier than a tennis ball. Suppose we throw a cricket ball and a tennis ball, both with the same speed or velocity. It will be found that more force is required to stop the cricket ball (Which has more mass) and less force is required to stop the tennis ball (which has less mass). We conclude that the force required to stop a moving body is directly proportional to its mass. If we throw two cricket balls of the same mass at different speeds or velocities, it will be found that more force is required to stop that cricket ball which is moving with higher velocity and less force is required to stop that cricket ball which is moving with higher velocity and less force is required to stop the cricket ball moving with lower velocity. So conclude that the force required to
Read more

LIGHT, Class X,, MCQ Part 1

                                                               MCQ'S MCQ Questions for Class 10 Science Light Reflection and Refraction with Answers Students can solve NCERT Class 10 Science Light Reflection and Refraction Latest Exam Pattern Multiple Choice Questions with Answers to know their preparation level. Question1. When light falls on a smooth polished surface, most of it (a) is reflected in the same direction            (b) is reflected in different directions (c) is scattered                                                                                    (d) is refracted into the second medium                                                                          Answer: a                                                                                                                      Q2. The image formed by reflection from a plane mirror is                                                            (a) real and inverted                                       
Read more